/ Accueil / Arithmétique / Fractions continues
Fractions continues
Algorithme de développement en fractions continuées
Dans ce dernier cas, il sera, dans un premier temps, transformé en fraction décimale D = A/B.
La fraction A/B est mise sous la forme A/B = c + 1/(a/b)
où c est la partie entière de A/B et a/b l'inverse de b/a = A/B - c.
On reprend avec a/b à la place de A/B.
Finalement x = c0+1/(c1+1/(c2+1/(c3...))) que l'on écrit X = [c0, c1, c2, c3, ...]
Exemples
La partie entière de A/B = 3.1415926 est 3 et on calcule A/B - 3 = 1415926/10000000.
L'inverse de 1415926/10000000. est a/b = 10000000/1415926
On reprend le procédé en mettant a/b à la place de A/B
2) 745/237 = [3, 6, 1, 33] = 3+ 1/(6+ 1/(1 + 1/33))
Les réduites successives sont
3 = 3/1 19/6 = 3+ 1/6 22/7 = 3+ 1/(6+ 1/1) et enfin 745/237 = 3+ 1/(6+ 1/(1 + 1/33))
Le calcul des réduites est simple :
| 3 | 6 | 1 | 33 | ||
| 0 | 1 | 3 | 1+6*3 = 19 | 22 | 745 |
| 1 | 0 | 1 | 0+6*1= 6 | 7 | 237 |
Calculs
Autres exemples
-
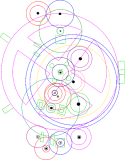
 Anticythère
Anticythère - 13.368267... approché par la fraction 254/19 dans le mécanisme des roues dentées (80 avant J.-C.) découvert en 1900 près de l'île d'Anticythère dans un navire romain par des pêcheurs d'éponge.
-
 Mois lunaire
Mois lunaire - Depuis le grec Meton, les astronomes savaient que le mois lunaire dure 29,530588... jours, que l'année tropique est de 365,242199... et donc qu'en une année le nombre de mois lunaires est de 12,368267....
-
 Nombre ln(2)/ln(3/2) de quintes dans une octave, solution de (3/2)n=2. Votre gamme dépendra de la fraction continue que vous choisirez : 5/3, 12/7 ?
Une quinte est l'intervalle entre les harmoniques 2 et 3 et correspond à un rapport de fréquence de 3/2, une octave est l'intervalle entre la fréquence de base et son harmonique 2.
Nombre ln(2)/ln(3/2) de quintes dans une octave, solution de (3/2)n=2. Votre gamme dépendra de la fraction continue que vous choisirez : 5/3, 12/7 ?
Une quinte est l'intervalle entre les harmoniques 2 et 3 et correspond à un rapport de fréquence de 3/2, une octave est l'intervalle entre la fréquence de base et son harmonique 2.
Précision des calculs
Les valeurs affichées (e, PI, sqrt(2) ...) sont en réalité, dans les calculs effectués, remplacées par des valeurs approchées qui ne sont que des nombres décimaux et absolument pas les nombres souhaités. C'est pour cela que seuls les premiers termes trouvés par le programme sont exacts, il convient donc de se méfier tout particulièrement des fractions dont le numérateur ou le dénominateur sont grands.
Lorsque le nombre est un décimal, il n'est pas toujours reconnu comme tel par le programme, aussi il est
préférable de l'écrire sous forme de fraction décimale, comparer les résultats obtenus en prenant la fraction décimale 1368267/1000000 ou l'écriture décimale 13.368267.
Calculs à l'aide de bc
(bc est une calculatrice en ligne de commande que vous trouverez dans toutes les distributions linux, elle se programme comme du C ou du javascript. Elle permet d'utiliser des nombres de décimales élevé, malheureusement elle n'a pas de fonction partie entière et la façon qu'elle a de fournir ou non des décimales n'est pas des plus pratiques).
Le premier programme donne la suite des entiers 3, 1, ... et le second programme donne les fractions continues successives.
Dans les lignes de commandes ci-dessous, 50000 est le nombre de décimales utilisées pour PI et les calculs qui suivront, le nombre 20 qui vient immédiatement après est le nombre d'itérations souhaité.
echo 50000 20 |bc spi.bc -l -q 3 7 15 1 292 1 1 1 2 1 3 1 14 2 1 1 2 2 2 (4 inexact ?) echo 50000 20 |bc frpi.bc -l -q 3/1 22/7 333/106 355/113 103993/33102 104348/33215 208341/66317 312689/99532 833719/265381 1146408/364913 4272943/1360120 5419351/1725033 80143857/25510582 165707065/52746197 245850922/78256779 411557987/131002976 1068966896/340262731 2549491779/811528438 6167950454/1963319607 (27221293595/8664806866 inexact ?)Mais ATTENTION, il reste à vérifier que les valeurs ainsi obtenues sont exactes ! Essayez peut-être, dans un premier temps, d'utiliser plus de décimales...
Il est préférable de choisir un algorithme plus efficace pour ces programmes à la place du calcul habituel des parties entières et des inverses des différences. Un tel algorithme se trouve ici, il suffirait de n'afficher que les fractions continues, les explications sont données dans la page.
Calculez 22/7 - 3 =1/7 puis 333/106 - 22/7 = -1/742 puis encore 355/113-333/106 = 1/11978, 103993/33102 - 355/113 ... et regardez bien les numérateurs que vous obtenez. Cette propriété est générale pour les fractions continues.
355/113 est due au chinois Zu Chong-Zhi (430 à 501).
Vous pourrez, c'est souvent même très facile, trouver des fractions p/q de dénominateurs q : 113 < q < 33102 qui seront comprises entre les deux frations continues : 103993/33102 < q < 355/113 et dont les valeurs seront plus proches de PI que ne l'est 355/113 (pas la seconde).
Mais aucune de ces fractions p/q n'approchera mieux PI que ne le font 355/113 et 103993/33102 dans le sens suivant :
calculez les valeurs absolues |355-113*PI|, |103993-33102*PI| et |p-q*PI| et comparez-les. Prenez par exemple la fraction intermédiaire p/q=89793/28582 et calculez |89793-28582*pi| = 0.0012249... qui est énorme comparé aux deux autres résultats !
(Toujours avec 113 < q < 33102, |p-q*PI| sera strictement supérieur à |103993-33102*PI| et aussi supérieur ou égal à |355-113*PI| ce qui montre que les fractions continues approchent excellemment bien les réels, lorsque l'on généralise la propriété).
|89793-28582*pi| = 0.0012249... |355-113*PI|= .00003014435... |103993-33102*PI| = 0.0000191293357
(Idem pour deux autres fractions continues successives).
Pour d'autres constantes que PI, changez la valeur utilisée par les programmes en modifiant le fichier source. Pour PI, c'est la ligne
pi=4*a(1); des programmes, c.-à-d. pi=4 arc tangente(1). Pour e écrivez e(1) et pour la
racine carrée de 2 mettez sqrt(2) ou e(l(2)/2), dans le langage bc.
Vous trouverez plus haut dans la marge une référence à l'encyclopédie en lignes des suites d'entiers. La suite A001203 est justement le développement de PI en fraction continue.
Suivez les liens au bas de la page OEIS pour mieux connaître ce développement de PI. W. Gosper calcule 204 103 termes en aout 1977 puis 17 001 303 termes en 1985.
La suite A032523 s'obtient en cherchant les rangs des premières apparitions des entiers 1, 2, 3, 4, 5, ... dans le développement de PI.
Autres pages
Liens
Voir également la collection de programmes de théorie des nombres à la page [Some BCMath/PHP number theory programs]
Plusieurs de ces programmes sont dédiés aux fractions continues :
Euclid's algorithm and the continued fraction expansion of a rational number; Guessing the simple continued fraction expansion of logba; Calculating the fraction represented by the simple continued fraction a0+1/a1+ ··· +1/an; Finding the simple continued fraction of a quadratic irrational; the continued fraction of the unique positive root > 1 of a polynomial with integer coefficients; a Sturm sequence for a squarefree polynomial; Factorising a non-negative unimodular matrix. Factorising a non-negative non-singular matrix. Finding the simple continued fraction of ep/q.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()