Accueil / Mots / Suites / Suites auto-génératrices
Suites auto-génératrices
Description
Ensemble auto-générateur, Nombre d'or et suite de Fibonacci
Dans le texte "A Self-Generating Set and the Golden Mean", Clark Kimberling définit une partie S de l'ensemble des entiers strictements positifs par :
la suite obtenue est la suite A052499 de Sloane.
En repérant les positions dans cette suite des puissances de 2 on trouve les rangs 0, 1, 3, 6, 11, 19 .., et en ajoutant 2 on tombe sur la suite 2, 3, 5, 8, 13, 21, de ... Fibonacci, d'où la formule S(F(n+3)-2)=2n de Henry Bottomley [Démo.]
[Cliquez pour observer cette construction]
Les rangs des termes pairs de cette suite forment la suite A000201 de Sloane. C'est une suite de Beatty, c'est très exactement la suite des parties entières de n fois le nombre d'or (1 + sqrt(5))/2.
[Cliquez pour cette construction], cette suite se trouve dans la partie II.
Les rangs des termes pairs de cette suite - excepté le rang 0 - forment la suite A001950 de Sloane, autre suite de Beatty.
[Cliquez pour cette construction].
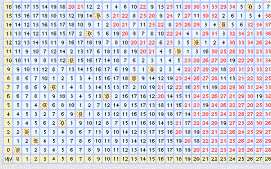
Ces deux suites permettent de trouver les coordonnées des cases gagnantes (marquées 0 sur la figure ci-contre) au jeu de Wythoff qui sont (0, 0), (1, 2), (3, 5), (4, 7), (6, 10), ... ou inversées (voir aussi les valeurs prises par la fonction de Grundy).
- 1 appartient à S
- si x est un élément de S, alors 2*x et 4*x-1 sont éléments de S
la suite obtenue est la suite A052499 de Sloane.
En repérant les positions dans cette suite des puissances de 2 on trouve les rangs 0, 1, 3, 6, 11, 19 .., et en ajoutant 2 on tombe sur la suite 2, 3, 5, 8, 13, 21, de ... Fibonacci, d'où la formule S(F(n+3)-2)=2n de Henry Bottomley [Démo.]
[Cliquez pour observer cette construction]
Les rangs des termes pairs de cette suite forment la suite A000201 de Sloane. C'est une suite de Beatty, c'est très exactement la suite des parties entières de n fois le nombre d'or (1 + sqrt(5))/2.
[Cliquez pour cette construction], cette suite se trouve dans la partie II.
Les rangs des termes pairs de cette suite - excepté le rang 0 - forment la suite A001950 de Sloane, autre suite de Beatty.
[Cliquez pour cette construction].
Ces deux suites permettent de trouver les coordonnées des cases gagnantes (marquées 0 sur la figure ci-contre) au jeu de Wythoff qui sont (0, 0), (1, 2), (3, 5), (4, 7), (6, 10), ... ou inversées (voir aussi les valeurs prises par la fonction de Grundy).
Mot de Fibonacci
En soustrayant 1 aux éléments de cette suite, puis en écrivant les nombres obtenus dans
la base 2, on montre que l'on obtient les nombres dont l'écriture binaire ne comporte
pas deux 0 adjacents A003754.
[Cliquez pour cette construction], ces écritures se touvent dans la partie II. ci-dessous.
L'ensemble S est repris par J.-P. Allouche, J. Shallit et G. Skordev dans l'article Self-generating sets, integers with missing blocks, and substitutions qui montrent que l'on obtient très simplement le mot infini de Fibonacci en étudiant la parité des termes de la suite (à partir du second)
[Cliquez pour observer cette construction].
Notez que l'application est capable de déterminer pour le mot "01001010010010100101..." un morphisme "0->01, 1->0" permettant de le construire à partir du premier caractère "0".
Remarque : Si le premier terme de la suite est conservé, on obtient le mot infini "101001010010010100101..." qui peut être engendré en utilisant le morphisme "1->10, 0->100", on peut retrouver cette construction sur l'une des pages du site dédiées à la suite de Fibonacci ou sur la page des morphismes et du monoïde libre.
[Cliquez pour cette construction].
[Cliquez pour cette construction], ces écritures se touvent dans la partie II. ci-dessous.
L'ensemble S est repris par J.-P. Allouche, J. Shallit et G. Skordev dans l'article Self-generating sets, integers with missing blocks, and substitutions qui montrent que l'on obtient très simplement le mot infini de Fibonacci en étudiant la parité des termes de la suite (à partir du second)
[Cliquez pour observer cette construction].
Notez que l'application est capable de déterminer pour le mot "01001010010010100101..." un morphisme "0->01, 1->0" permettant de le construire à partir du premier caractère "0".
Remarque : Si le premier terme de la suite est conservé, on obtient le mot infini "101001010010010100101..." qui peut être engendré en utilisant le morphisme "1->10, 0->100", on peut retrouver cette construction sur l'une des pages du site dédiées à la suite de Fibonacci ou sur la page des morphismes et du monoïde libre.
[Cliquez pour cette construction].
Application
Quelques exemples
Ensembles
[Multiples de 3],
[B],
[C],
[D],
[E],
[F],
Exclusion des nombres dont l'écriture [en base 2 contient 00], puis ces nombres [convertis en base 10]
Factorisations
Retrouvez des morphismes permettant d'obtenir les mots infinis suivants :
[Mot de Prouhet-Thue-Morse],
[Mot de Tribonacci],
[Mot de Rudin-Shapiro],
[Mot quelconque]
[FACTORISE]
Liens
A Self-Generating Set and the Golden Mean Clark Kimberling, University of Evansville - Journal of Integer Sequences, Vol. 3 (2000), Article 00.2.8
Self-generating sets, integers with missing blocks, and substitutions J.-P. Allouche, J. Shallit, G. Skordev. Dicrete Math. 292 (2005), 1-15.
Exclusion des nombres dont l'écriture [en base 2 contient 00], puis ces nombres [convertis en base 10]
Retrouvez des morphismes permettant d'obtenir les mots infinis suivants :
[Mot de Prouhet-Thue-Morse], [Mot de Tribonacci], [Mot de Rudin-Shapiro], [Mot quelconque]
[FACTORISE]
[Mot de Prouhet-Thue-Morse], [Mot de Tribonacci], [Mot de Rudin-Shapiro], [Mot quelconque]
[FACTORISE]
Liens
A Self-Generating Set and the Golden Mean Clark Kimberling, University of Evansville - Journal of Integer Sequences, Vol. 3 (2000), Article 00.2.8
Self-generating sets, integers with missing blocks, and substitutions J.-P. Allouche, J. Shallit, G. Skordev. Dicrete Math. 292 (2005), 1-15.
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.