Arbre de Stern-Brocot
l'arbre dit de Stern-Brocot a été découvert en 1858 (Über eine zahlentheoretische Funktion. Crelle's Journal 55:193-220) par le mathématicien allemand Moritz Stern (1807-1894) et de manière indépendante en 1861 (Calcul des rouages par approximation, nouvelle méthode. Revue Chronométrique 3:186-194) par l'horloger français Achille Brocot (1817-1878) [DMA].
Description
Fraction médiante
 L'arbre de Stern-Brocot représenté ci-contre contient toutes les fractions irréductibles strictement
positives a/b et uniquement ces fractions. (Le numérateur a et se dénominateur b sont deux naturels premiers entre-eux).
L'arbre de Stern-Brocot représenté ci-contre contient toutes les fractions irréductibles strictement
positives a/b et uniquement ces fractions. (Le numérateur a et se dénominateur b sont deux naturels premiers entre-eux).
Si tout en haut de l'arbre, on place la fraction 0/1 à l'extrême gauche et l'écriture 1/0 à droite, on explique plus aisément la manière de construire l'arbre de Stern-Brocot :
Chaque fraction est la médiante1
m a + c a c --- = --------- médiante de --- et de --- n b + d b d
des deux fractions situées au-dessus de m/n, les plus proches horizontalement, a/b à gauche et c/d à droite.
(1) Edouard Lucas, à la p. 467 de son ouvrage "Théorie des nombres" de 1891, utilise la même définition et dit : « nous obtenons une fraction que nous appellerons la médiante des deux premières ». Quelques lignes plus loin : « Ainsi par ce procédé dit de médiation, dont on trouve de nombreux exemples dans les ouvrages d'Archimède et des géomètres de l'Inde, nous formons... ».
On obtient par exemple 3/5 à partir de 1/2 à gauche et 2/3 à droite en calculant le numérateur 3 = 1+2 et le dénominateur 5 = 2+3.
La moitié gauche de la liste ordonnée de toutes les fractions des k premiers niveaux confondus est une suite comme celle-ci : [Cliquer]
Le numérateur de la fraction médiante obtenue est la somme des numérateurs des deux fractions. Le dénominateur est la somme des dénominateurs.
On démontre aisément cette propriété par récurrence : de bc-ad=1 on déduit ab-ab + bc-ad=1, c.-à-d. b(a+c)-a(b+d)=1 au rang n+1 ...
Suites de Farey
Les suites de Farey Fk s'obtiennent en ne conservant que les fractions de dénominateur
inférieur ou égal à k comprises entre 0/1 et 1/1 comme dans
 ou encore
ou encore

On obtient aussi la suite de Farey Fk en insérant les fractions de dénominateur k dans la suite Fk-1, comme médiantes de deux fractions de Fk-1.
On a donc encore la propriété bc-ad=1 pour a/b et c/d consécutives dans Fk.
On obtient aussi la suite de Farey Fk en insérant les fractions de dénominateur k dans la suite Fk-1, comme médiantes de deux fractions de Fk-1.
On a donc encore la propriété bc-ad=1 pour a/b et c/d consécutives dans Fk.
Système de numération
En notant les mouvements L vers la gauche et R vers la droite (L=left, R=right)
lorsqu'on parcourt l'arbre depuis sa racine 1/1 jusqu'à la fraction a/b,
on obtient un mot utilisant les lettres l'alphabet binaire {L, R}.
Ce mot représente le rationnel a/b.
Le mot vide code le rationnel 1/1.
Par exemple 4/7 = LRLL = LRL2. Le parcours passe par les fractions 1/1 la racine, 1/2, 2/3, 3/5 et 4/7.
Ce mot représente le rationnel a/b.
Le mot vide code le rationnel 1/1.
Par exemple 4/7 = LRLL = LRL2. Le parcours passe par les fractions 1/1 la racine, 1/2, 2/3, 3/5 et 4/7.
Développement en fraction continue
Soit le réel x>0 correspondant au mot Ra0 La1 Ra2 La3 ...
(On commence toujours par Ra0 et a0 est éventuellement nul contrairement à a1, a2 ... qui sont strictement positifs).
Le réel x a pour développement en fraction continue [a0 ; a1, a2, a3 ... ] c'est-à-dire a0+1/(a1+1/(a2+1/(a3+ ...))).
Les réduites du développement de x sont obtenues dans le parcours de l'arbre de Stern-Brocot, elles encadrent x au plus près, alternativement inférieures et supérieures à x. Si, par exemple la fraction rk< x est une réduite, la fraction suivante du parcours, ou même plusieurs fractions successives, sont supérieures à x, la plus petite de ce groupe est la prochaine réduite rk+1 > x. On en déduit un algorithme de recherche des fractions continues bien plus efficace que celui qui calcule la partie entière et l'inverse de la partie décimale.
Par exemple la nombre exp(1) = e = 2,7182818... base des logarithmes népériens, se développe en R2L1R2L1R1L4R1L1R6L1R1L8R1L1R10... et a pour fraction continue [ 2 ; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, ...] = 2+1/(1 +1/(2 +1/(1+1/(4+1/(1+1(6+...)))))), on devine la suite, Euler a démontré la propriété en partant de la fraction continue de th(1/2).
Les réduites de e sont 2/1, 3/1, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, 299/110, 1264/465 etc. Repérez leurs positions parmi les fractions obtenues.
Plus généralement, le développement en fraction continue de el/m où l et m sont entiers strictement positifs, n'est connu que pour quelques valeurs particulières de l et de m (l/m irréductible et l=1 ou l=2).
L'algorithme développé en 1978 par L. Davison [DA] utilise une décomposition de matrices en produits des matrices L, R (qui correspondent exactement au parcours dans l'arbre de Stern-Brocot).
Une implémentation a été réalisée par Keith Matthews [KM] dans les langages bc et php (extension).
(On commence toujours par Ra0 et a0 est éventuellement nul contrairement à a1, a2 ... qui sont strictement positifs).
Le réel x a pour développement en fraction continue [a0 ; a1, a2, a3 ... ] c'est-à-dire a0+1/(a1+1/(a2+1/(a3+ ...))).
Les réduites du développement de x sont obtenues dans le parcours de l'arbre de Stern-Brocot, elles encadrent x au plus près, alternativement inférieures et supérieures à x. Si, par exemple la fraction rk< x est une réduite, la fraction suivante du parcours, ou même plusieurs fractions successives, sont supérieures à x, la plus petite de ce groupe est la prochaine réduite rk+1 > x. On en déduit un algorithme de recherche des fractions continues bien plus efficace que celui qui calcule la partie entière et l'inverse de la partie décimale.
Par exemple la nombre exp(1) = e = 2,7182818... base des logarithmes népériens, se développe en R2L1R2L1R1L4R1L1R6L1R1L8R1L1R10... et a pour fraction continue [ 2 ; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, ...] = 2+1/(1 +1/(2 +1/(1+1/(4+1/(1+1(6+...)))))), on devine la suite, Euler a démontré la propriété en partant de la fraction continue de th(1/2).
Les réduites de e sont 2/1, 3/1, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, 299/110, 1264/465 etc. Repérez leurs positions parmi les fractions obtenues.
Plus généralement, le développement en fraction continue de el/m où l et m sont entiers strictement positifs, n'est connu que pour quelques valeurs particulières de l et de m (l/m irréductible et l=1 ou l=2).
L'algorithme développé en 1978 par L. Davison [DA] utilise une décomposition de matrices en produits des matrices L, R (qui correspondent exactement au parcours dans l'arbre de Stern-Brocot).
Une implémentation a été réalisée par Keith Matthews [KM] dans les langages bc et php (extension).
Exemples
Fraction associée à un mot
LRLRLRLR
L2RL2RL2RL2RL2RL2RL2RL2R
LRLR2LR3LR4LR5LR6
Mot associé à une fraction
Mot associé à la valeur réelle d'une expression
2/3 (valeur approchée par un décimal 0,6...6 et non une valeur exacte, le mot obtenu a été limité volontairement aux 1000 premiers caractères !)
exp(1) = e base des logarithmes népériens. e^2 e^-1 PI PI^2 1/PI racine(2) 1/racine(2) racine(3) racine(5) racine(6) racine(7) racine(8) racine(10) ln(2)
Avec le nombre d'or (racine(5)+1)/2 observez comment les numérateurs et dénominateurs vous donnent la suite de Fibonacci pour un parcours RLRLR... très simple de l'arbre.
exp(1) = e base des logarithmes népériens. e^2 e^-1 PI PI^2 1/PI racine(2) 1/racine(2) racine(3) racine(5) racine(6) racine(7) racine(8) racine(10) ln(2)
Avec le nombre d'or (racine(5)+1)/2 observez comment les numérateurs et dénominateurs vous donnent la suite de Fibonacci pour un parcours RLRLR... très simple de l'arbre.
Suite des fractions
Approximations successives par les fractions de l'arbre de Stern-Brocot
d'un nombre donné. (Elles sont données dans les exemples des paragraphes ci-dessus).
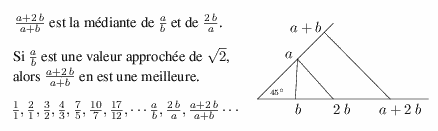
L'exemple ci-dessus reprend le calcul approché de la racine carrée de 2 par Théon de Smyrne mais avec une petite modification : chaque fraction a/b est suivie par la fraction [2b/a] qui s'insére alors dans la suite originale, ceci pour permettre de retrouver toutes les fractions du chemin RLLRRLL... de l'arbre de Stern-Brocot.
On part de 1/1 et on effectue les calculs a/b, [2b/a], (a+2b)/(a+b), [2(a+b)/(a+2b)] ...
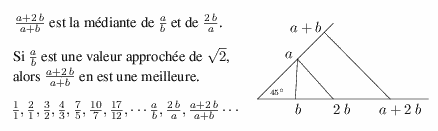
L'exemple ci-dessus reprend le calcul approché de la racine carrée de 2 par Théon de Smyrne mais avec une petite modification : chaque fraction a/b est suivie par la fraction [2b/a] qui s'insére alors dans la suite originale, ceci pour permettre de retrouver toutes les fractions du chemin RLLRRLL... de l'arbre de Stern-Brocot.
On part de 1/1 et on effectue les calculs a/b, [2b/a], (a+2b)/(a+b), [2(a+b)/(a+2b)] ...
Documents – Compléments – Liens
Fichier LATEX (nécessitant l'extension ecltree) et le programme qui permet de générer automatiquement ce fichier LATEX, quel que soit le nombre de niveaux souhaités de l'arbre.
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()