Vous êtes ici : Accueil/Jeux/Solitaires/Échanges de cavalaiers
Échange des cavaliers
Le jeu
Présentation
Pour résoudre ce casse-tête vous devez échanger les positions des deux cavaliers rouges avec celles des deux noirs, en respectant évidemment les règles du déplacement du cavalier sur un échiquier et en n'utilisant que les dix cases dessinées.
Échiquier
Cliquez d'abord sur le cavalier à déplacer et ensuite sur la case libre où il doit aller.
Solution
Un graphe
Une méthode simple permet de trouver rapidement la solution. Elle consiste à dessiner autrement le graphe dont les dix sommets représentent les cases de l'échiquier et dont les arêtes correspondent aux sauts des cavaliers.
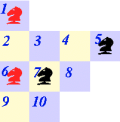
La première figure fait correspondrent les cases aux nombres entiers de 1 à 10, les sommets du graphe non-orienté représenté sur la figure suivante.
Sur la figure de droite les sommets reliés par une arête sont placés près l'un de l'autre, la figure obtenue est bien plus simple à étudier.

La première figure fait correspondrent les cases aux nombres entiers de 1 à 10, les sommets du graphe non-orienté représenté sur la figure suivante.
Sur la figure de droite les sommets reliés par une arête sont placés près l'un de l'autre, la figure obtenue est bien plus simple à étudier.


Déplacements successifs
Les déplacements d'une solution en 40 coups sont :
Cavalier Rouge 1 - 4 - 10 - 2 - 8
Cavalier Noir 7 - 1 - 4 - 10 - 2
Cavalier Noir 5 - 7 - 1 - 4 - 10
Cavalier Rouge 6 - 4 - 1 - 7 - 5
Cavalier Noir 10 - 4 - 1 - 7
Cavalier Noir 2 - 10 - 4 - 1
Cavalier Rouge 8 - 2 - 10 - 4 - 6
Cavalier Noir 1 - 4 - 10 - 2
Cavalier Noir 7 - 1 - 4 - 10
Cavalier Rouge 6 - 4 - 1 - 7
Cavalier Noir 10 - 4 - 1
Cavalier Noir 2 - 10 - 4 - 6
Cette solution n'utilise pas les deux cases 3 et 9 de l'échiquier.
Parcours d'un cavalier sur tout un échiquier
Un cycle hamiltonien du graphe
Pour un échiquier de 6 cases de côté, les sommets sont les 64 cases de l'échiquier et plus généralement, pour un échiquier de n cases de côté, le nombre de sommets du graphe est n×n = n2. En repérant les cases par leurs deux coordonnées i et j, le sommet (i, j) est relié par une arête aux huit sommets (i-1, j-2), (i+1, j-2), (i-2, j-1), (i+2, j-1), (i-1, j+2), (i+1, j+2), (i-2, j+1), (i+2, j+1), lorsque ceux-ci ne sont pas à l'extérieur de l'échiquier.
Chercher un parcours du cavalier qui passe une fois et une seule par toutes les cases de l'échiquier, correspond à la recherche d'un chemin hamiltonien sur le graphe : un chemin passant une fois et une seule par tous les sommets du graphe. (Si l'on peut revenir à la case de départ en une étape supplémentaire, il s'agit alors d'un cycle hamiltonien).
Chercher un parcours du cavalier qui passe une fois et une seule par toutes les cases de l'échiquier, correspond à la recherche d'un chemin hamiltonien sur le graphe : un chemin passant une fois et une seule par tous les sommets du graphe. (Si l'on peut revenir à la case de départ en une étape supplémentaire, il s'agit alors d'un cycle hamiltonien).
Exemple
Pour un échiquier de 6 cases de côté le graphe est le suivant :
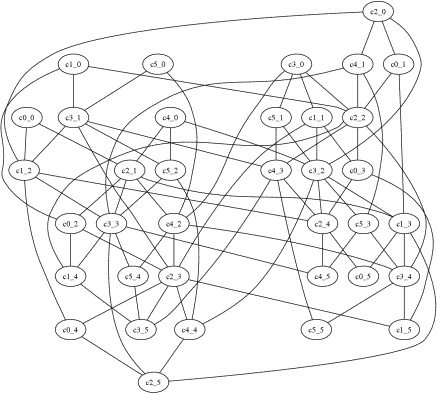
Si vous désirez chercher à la main un cycle, considérez le plus tôt possible les quatre coins : les sommets notés c0_0=(0, 0), c0_5=(0, 5), c5_0=(5, 0) et c5_5=(5, 5) sur l'image ci-dessus.
Les graphes des six échiquiers de 3 à 8 cases de côtés se trouvent dans le fichier grnn.pdf.
Des définitions et des explications complémentaires se trouvent dans le cours sur la théorie des graphes. Le parcours du cavalier y est traité à la page 10 et on y trouve aussi un programme cavalier.c de recherche de tous les chemins hamiltoniens possibles du cavalier, les solutions sont obtenues sous la forme :

Si vous désirez chercher à la main un cycle, considérez le plus tôt possible les quatre coins : les sommets notés c0_0=(0, 0), c0_5=(0, 5), c5_0=(5, 0) et c5_5=(5, 5) sur l'image ci-dessus.
Les graphes des six échiquiers de 3 à 8 cases de côtés se trouvent dans le fichier grnn.pdf.
Des définitions et des explications complémentaires se trouvent dans le cours sur la théorie des graphes. Le parcours du cavalier y est traité à la page 10 et on y trouve aussi un programme cavalier.c de recherche de tous les chemins hamiltoniens possibles du cavalier, les solutions sont obtenues sous la forme :
0 15 6 25 10 13 Compilation du programme C :
33 24 11 14 5 26 cc -o cavalier cavalier.c
16 1 32 7 12 9 Utilisation du programme :
31 34 23 20 27 4 cavalier 6
22 17 2 29 8 19 (le premier chemin obtenu est la solution ci-contre, à gauche)
35 30 21 18 3 28
Dans la solution ci-dessus, les positions successives sont notées 0, 1, 2, ..., 35. (Vérifiez qu'il s'agit d'un chemin hamiltonien et non d'un cycle).
Un peu d'histoire
Voir la page de liens consacrée à Sir William Rowan Hamilton (Dublin 1805 -1865).
Hamilton découvrit aussi les quaternions, (corps non-commutatif dans lequel i2 = j2 = k2 = ijk = -1). On trouvera des références à la page de liens et un exemple utilisant certains quaternions à la page Loi de composition interne ainsi d'ailleurs que bien d'autres exemples, tels les complexes et les octonions).
On doit aussi à Hamilton l'énoncé du théorème dit de Cayley-Hamilton et sa démonstration dans le cas d'un espace vectoriel de dimension 2. C'est Frobenius qui le démontre pour tous les espaces vectoriels de dimensions finies.
Théorème : étant donnés un espace vectoriel E de dimension finie sur C, u un endomorphisme de E (application linéaire de E dans E) et P le polynôme caractéristique de u. Alors P(u) = 0.
Lorsque l'endomorphisme u est connu par sa matrice M, on a P(M)=0 (matrice nulle), voir la page Calcul matriciel du site pour des exemples
Hamilton découvrit aussi les quaternions, (corps non-commutatif dans lequel i2 = j2 = k2 = ijk = -1). On trouvera des références à la page de liens et un exemple utilisant certains quaternions à la page Loi de composition interne ainsi d'ailleurs que bien d'autres exemples, tels les complexes et les octonions).
On doit aussi à Hamilton l'énoncé du théorème dit de Cayley-Hamilton et sa démonstration dans le cas d'un espace vectoriel de dimension 2. C'est Frobenius qui le démontre pour tous les espaces vectoriels de dimensions finies.
Théorème : étant donnés un espace vectoriel E de dimension finie sur C, u un endomorphisme de E (application linéaire de E dans E) et P le polynôme caractéristique de u. Alors P(u) = 0.
Lorsque l'endomorphisme u est connu par sa matrice M, on a P(M)=0 (matrice nulle), voir la page Calcul matriciel du site pour des exemples
- 1) cliquer sur le 1er bouton [Matrice au hasard] pour obtenir aléatoirement une matrice carrée réelle puis
- 2) cliquer sur [Polynôme caract. P] pour obtenir le polynôme caractéristique P que l'on peut lire dans la fenêtre d'affichage de l'application, sous la matrice, enfin
- 3) cliquer sur le dernier bouton [Cayley-Hamilton] de l'application pour obtenir P(M) qui est bien la matrice nulle.
Documents compléments références liens divers
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()