/ Accueil / Probabilités / Paradoxe de Parrondo

Paradoxe de Parrondo

Paradoxe ?

Le physicien Juan M.R. Parrondo est l'inventeur du paradoxe du même nom. On trouvera un exposé en anglais sur sa page personnelle. Il s'agit d'un jeu relativement complexe que l'on présente comme une succession de lancers de pièces de monnaies non équilibrées. Il est la combinaison du jeu A, simple lancer d'une pièce n° 1, et du jeu B où on lance soit la pièce n° 2 soit la n° 3 :

Fig1. Jeux A et B

Les deux jeux A et B

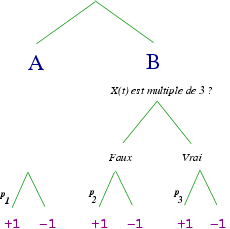
A est un lancer d'une pièce de monnaie où Face est gagnante avec la probabilité p₁=1/2-e, le gain est alors d'un euro. Pile est perdante avec la probabilité 1-p₁=1/2+e (gain de -1 euro).
B est un peu plus compliqué, si le capital est multiple de 3, alors Face gagne avec la probabilité p₃=1/10-e, sinon Face gagne avec la probabilité p₂=3/4-e

Lorsque e = 0, le jeu A, joué seul, est équitable. Toujours lorsque e = 0, le jeu B tend à devenir équitable lorsque le nombre n de parties croît indéfiniment (Cliquez sur 'calcule A' ou sur 'calcule B').
Les deux jeux A et B, joués seuls, sont perdants lorsque e > 0.

Cliquez sur 'simule A' ou sur 'simule B' pour lancer les simulations.
Les valeurs presque exactes (les erreurs d'arrondi sont souvent inévitables), s'obtiennent ensuite en cliquant le bouton [Calcule].

Combinaisons des deux jeux

Fig. 2 Gains moyens dans B+, (AB)+, (AAB)+ (e=0)

Lorsqu'on utilise des combinaisons répétées comme (AABB)+ ou encore (AAABBAB)+, on observe que le jeu devient gagnant pour certaines de ces combinaisons, ce qui peut sembler contre-intuitif !

Évidemment le jeu n'est paradoxal qu'en apparence, les résultats observés se calculent aisément et le 'paradoxe' s'explique finalement par la non-commutativité du produit de certaines matrices (les matrices de transition).
Qui songerait à trouver paradoxal qu'un produit matriciel M×N soit différent de N×M ?

On peut d'ailleurs concevoir facilement d'autres jeux, plus simples, ayant le même type de comportement [EZ].

Simulations et calculs

Vous pouvez modifier certains paramètres et calculer le gain moyen en effectuant au choix :

un certain nombre de simulations de lancers de pièces de monnaies
le calcul au moyen des matrices de transition.

Parrondo

Exemples

Quel est le mot répété le plus avantageux ?

Simulations :   AAAAA, AAAAB, AAABB, AABAB, AABBB, ABABB, ABBBB, BBBBB

Simulations :   AAAAAA, AAAAAB, AAAABB, AAABAB, AABAAB, AAABBB, AABBAB, ABBAAB, AABBBB, ABABBB, ABBABB, ABBBBB BBBBBB

Mots de Fibonacci itérés, calculs :   BA, BAB, BABBA, BABBABAB, BABBABABBABBA, BABBABABBABBABABBABAB BABBABABBABBABABBABABBABBABABBABBA

A et B choisis au hasard

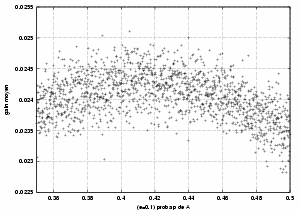
Les simulations sont effectuées en choisissant A au hasard avec la probabilité p indiquée en abscisse. Les probabilités sont p₁=1/2-e, p₂=3/4-e, p₃=1/10-e. Les deux cas correspondent à e=0.001 et à e=0.005.
Chaque point indiqué sur l'image a nécessité 10⁷ tirages. (Fig. 3)

La valeur optimale de p semble proche de la valeur p=0.4145 calculée par Doron Zeilberger et indiquée dans son papier, (avec e=0.001 semble-t-il).
programme C

Fig. 3 Simulations

Mots de Fibonacci (non répétés).

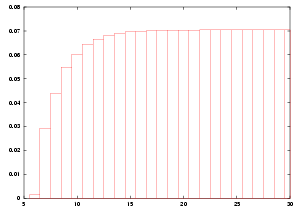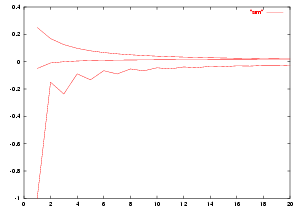
La figure (Fig 4.) indique les gains moyens correspondants à des mots de Fibonacci de tailles croissantes, de M₆=BABBABABBABBA à M₃₀ lorsque e=0.
La longueur du mot M₃₀ est 1346269 et le gain moyen est de 0.070423168.

Ces gains semblent rester inférieurs à ceux obtenus en concaténant plusieurs mots de Fibonacci M₅=BABBA. On arrive dans ce cas, toujours pour e=0, à des gains moyens d'environ 0.07567.

Fig 4. Mots de Fibonacci

Références, liens

Page personnelle de Juan M.R. Parrondo

Brownian Ratchets, Parrondo's Games and more... Greg Harmer - Two games with unusual properties were originally devised by Prof. Juan MR Parrondo as a pedagogical example of a Brownian ratchet.

Parrondo's Paradox Dan Vellerman and Stan Wagon. Two losing games can combine into a winning game. wagon93.nb (317.8 KB) - Mathematica Notebook

Etats d'A M E - Le paradoxe de Parrondo Journal de l'Association des Mathématiciens de l'École Polytechnique Fédérale de Lausanne - Numéro 9 - Oct. 2002

Hasard mathématique et chaos biologique Hervé Ratel - Qui perd gagne - Sciences & Avenir Avril 2000 -- N° 638. Tentez votre chance à un jeu de hasard. Le plus souvent, vous perdez. Jouez à deux jeux de hasard, alternativement et de façon aléatoire : surprise, vous gagnez ! Ce paradoxe éclaire les mécanismes apparemment chaotiques, et pourtant bien huilés, des cellules ou des protéines.
Le paradoxe sert à expliquer, comment le caractère chaotique du mouvement brownien dans les cellules peut promouvoir l'évolution. Jusqu'à présent on pensait toujours que ce désordre empêchait toute amélioration des structures.

Parrondo Paradox cut-the-knot.com Alexander Bogomolny

Brownian Motor Roland Ketzmerick, Matthias Weiß, Franz-Josef Elmer, Roland Ketzmerick, Franz-Josef Elmer, Franz-Josef Elmer

On-line Simulator for Parrondo's Paradox Lee Spector (lisp + cgi program ?)

[EZ] Remarks On the PARRONDO PARADOX By Shalosh B. EKHAD and Doron Zeilberger

Parrondo's Paradox Eric Weisstein (MathWorld)

Winning With Losing Games   By John Allen Paulos Special to ABCNEWS.com. A New Paradox in the World of Probability
The Paradox of Parrondo's Games   Peter Taylor
On Parrondo's Paradox   - Optimal Adaptive Strategies for Games of the Parrondo Type - by Sven Rahmann (technical report, MATLAB functions, documentation)

Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.

Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.

J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.