Accueil/Jeux/Jeux logiques/Wyx
Le jeu de Wyx
Description
Visitez le site de Wyx, si vous jouez seul, procurez-vous les grilles du jeu et excercez-vous. Vous pourrez aussi jouer en ligne sur une centaine de grilles Wyx.
Wyx est un jeu mathématique pour tous publics, certaines grilles parmi les moins compliquées
peuvent être résolues par des enfants. Wyx permet d'aborder le plus simplement possible
un grand nombre de notions mathématiques diverses, en géométrie ce sont la translation plane,
les vecteurs et la somme vectorielle, en théorie des graphes ce sont les chemins
hamiltoniens multicolores (ou arcs-en-ciel)...
Rechercher une solution incite à élaborer des algorithmes réfléchis, justifiés et efficaces, c'est-à-dire à faire des mathématiques.
Grille
La case de départ est marquée d'un cavalier
Dominos
Dans ses déplacements, le cavalier devra effectuer une fois et une seule chacun des 12 déplacements. Les grilles sont construites pour qu'il y ait une solution et une seulement.
Exemple

Résolution
Arc-en-ciel
Case d'arrivée
(En effet l'addition des vecteurs est associative et commutative).
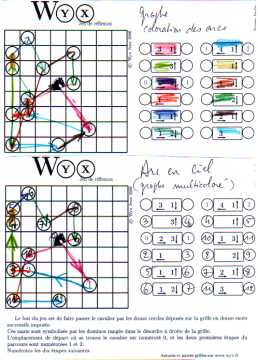
Le but du jeu
Par exemple, l'application placée plus bas dans la page m'indique pour une certaine grille cette solution :
Points : A L F K G H E C B D J I M
Vecteurs : i k e h f a l g j c d b
Le jeu est constitués de 13 points que l'on peut appeler
A B C ... K L M et de 12 dominos appelés de même a b c d ... j k l.
Le chemin trouvé passe par les points 13 points, non pas dans l'ordre alphabétique, mais dans l'ordre A L F K G H E C B D J I M, en utilisant successivement les dominos dans l'ordre i k e h f a l g j c d b.
En effet, pour ce jeu, le domino i permet d'aller du point de départ A au point L (second de la liste), ensuite le domino k permet de joindre L à F, puis e de F à K et ainsi de suite.
Un graphe
A=cavalier=départ, B, C, ..., K, L, M=arrivée, les 13 cases marquées sur l'échiquier.
Appelons aussi
a, b, c, ..., k, l, les 12 dominos, les déplacements ou leurs vecteurs.
Très généralement, lorsqu'un domino u permet d'aller d'une certaine case P vers une autre case Q, tracez une flèche de P vers Q sur la figure.
Mieux, coloriez avec 12 couleurs toutes les flèches, en choisissant une seule et même couleur pour les flèches qui correspondent à un même domino.
Finalement vous obtenez la figure d'un graphe orienté G dont l'ensemble des sommets est {A, B, C, ..., L, M} et dont les arcs sont coloriés à l'aide de 12 couleurs.
La solution du jeu est un chemin hamiltonien multicoloré du graphe, passant par tous les sommets de A à M et empruntant un arc et un seul de chaque couleur disponible (ce sous-graphe est un arc-en-ciel).
Méthode
Tableau
Par exemple, ci-dessous, à l'intersection de la ligne E et de la colonne J, se trouve la couleur f.
(Sur la grille de Wyx, le domino f permet d'aller de la case E à la case J).
A B C D E F G H I J K L M
--+---------------------------
A | c
B | k e
C | l e b j
D | c j
E | d j e f
F | h a
G | j g
H | l d
I | a
J | a l
K | e i
L | f i
M | a c
Algorithme
Commencez par effectuer une fois pour toute les deux manipulations ci-dessous.
- Effacez la dernière ligne, celle de M, en effet le point M est le point d'arrivée.
- Pour une raison similaire, effacez la première colonne, celle du point de départ.
La méthode proposée consiste à effacer successivement, par un raisonnement adapté, les couleurs à l'intérieur du tableau jusqu'à ne conserver que 12 noms différents, une par ligne et une par colonne, on aura alors une solution.
- Lorsqu'il n'y a qu'une seule couleur 'u' sur une ligne, alors elle apparaîtra dans la solution, à cet endroit et pas ailleurs.
- Effacez tous les autres 'u' du tableau.
- Effacez tous les autres couleurs de la colonne de 'u' (mais pas 'u', elle fait partie de la solution)
- De même, lorsqu'il n'y a qu'une seule couleur 'u' inscrite dans une colonne
- Effacez les autres 'u' du tableau.
- Effacez les autres couleurs de la ligne de 'u'
- Si la couleur 'u' ne figure que dans une seule case du tableau, effacez toutes les autres couleurs de sa ligne et de sa colonne.
- Si vous observez qu'une ligne ou une colonne est vide, alors il n'y a pas de solution. (Dans le tableau de 12 lignes et 12 colonnes, pas dans le tableau initial).
- Si un circuit XY...Z apparaît entre deux ou plusieurs points, alors vous n'obtiendrez plus de chemin hamiltonien dans cette grille. Rejetez cette grille.
- On n'arrive pas toujours directement au résultat à l'aide des manipulations précédentes. Si vous n'arrivez plus à progresser, choisissez une ligne ou une colonne contenant le moins possible de couleurs et faites autant de copies de votre tableau, mais ne gardez dans les différentes copies qu'une seule des couleurs de cette ligne ou de cette colonne.
Reprise du tableau
B C D E F G H I J K L M il ne reste que 12 lignes et 12 colonnes
--+-------------------------
A | c <-- 1) c est seul sur la ligne
B | k e
C | e b j
D | c j <-- 1) effacez c, le j reste seul
E | j e f
F | h a
G | g <-- 2) observez
H | l d
I | a <-- 3) observez
J | a<--1) effacez l
K | e i
L | f i
Exemples
L'application vous donne les coordonnées des points et des vecteurs, un schéma des positions des points dans le plan et le tableau à simplifier. Le point de départ est A, le point d'arrivée est M, les autres points et les vecteurs sont donnés dans le désordre.
Pour obtenir la solution, cochez à tout moment la petite case de droite. L'application ne donne qu'une solution même s'il en existe plusieurs. Dans tous les cas le nombre de solutions existantes est indiqué.
Utilisez les flèches
<- et -> pour retrouver les exemples précédents.
(x, y), -4≤x≤4, -4≤y≤4, et différents de (0, 0), (±3, ±3), (±3, ±4), (±4, ±4).
Les points doivent être tous contenus dans un carré de 8×8=64 points.
Ne vous privez pas d'utiliser ces grilles, plus de 2×108 sont produites à la minute par l'équivalent, en C, du programme ci-dessus.
Prolog
Prolog est tout à fait indiqué pour résoudre ce problème, on appréciera la grande simplicité de la programmation Prolog.
wyx(_, [], _, []) :- !.
wyx(DOMINOS, LOCATIONS, p(ACTU_X, ACTU_Y), [NEW_POS|SOLUTION_INTER]) :-
select(d(X, Y), DOMINOS, RES_DOMINOS),
NEW_X is ACTU_X + X,
NEW_Y is ACTU_Y - Y,
NEW_POS = p(NEW_X, NEW_Y),
select(NEW_POS, LOCATIONS, RES_LOCATIONS),
wyx(RES_DOMINOS, RES_LOCATIONS, NEW_POS, SOLUTION_INTER).
problem(SOLUTION) :-
DOMINOS = [d(-1, +4), d(+2, -1), d(-2, -2), d(+3, -2), d(0, -1), d(0, +1), d(-3, +1), d(+1, -1), d(-2, -1), d(0, +2), d(+2, +3), d(-2, 0)],
LOCATIONS = [p(1, 0), p(1, 3), p(2, 4), p(3, 4), p(4, 4), p(4, 5), p(6, 5), p(1, 6), p(2, 6), p(4, 6), p(6, 6), p(2, 7)],
ORG = p(3, 3),
wyx(DOMINOS, LOCATIONS, ORG, SOLUTION).
Les données du problème doivent être indiquées dans DOMINOS, LOCATIONS, ORG. On peut exécuter ce programme en utilisant SWI Prolog (par exemple en ligne de commande :
swipl -s wyx.pl). On indique ensuite problem(S). pour obtenir les solutions :
wyx$ swipl -s wyx.pl % library(swi_hooks) compiled into pce_swi_hooks 0.00 sec, 3,856 bytes ... ?- problem(S),print(S). [p(3,4),p(1,6),p(2,7),p(4,4),p(1,3),p(4,5),p(6,6),p(6,5),p(4,6),p(2,6),p(2,4),p(1,0)] S = [p(3, 4), p(1, 6), p(2, 7), p(4, 4), p(1, 3), p(4, 5), p(6, 6), p(6, 5), p(..., ...)|...]
Documents, compléments, liens
Sur le site
Sur d'autres sites
Vous trouverez sur ce site tous les renseignements sur Wyx et vous pourrez télécharger les feuilles de jeu. Vous pourrez aussi jouer en ligne sur une centaine de grilles Wyx.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()