Accueil / Mots / Suites / Suites de Hofstadter
Suites de Douglas Hofstadter
(Retour à l'Index général des suites)
Une suite chaotique
La première de ces suites est extraite du livre 'Gödel Escher Bach' de Douglas Hofstadter (pages 154-155 de la version française).
C'est la suite
A005185 de
N.J.A. Sloane, appelée "The Hofstadter Q-sequence".
Un peu à la manière des suites de Fibonacci et de Lucas, chaque terme est la somme de deux termes précédents, mais pas les deux termes immédiatement précédents :
(La définition de la suite de Fibonacci est plus simple : F(n) = F(n-1) + F(n-2)).
Page avec l'applet java de la suite Q
Exemple : calcul de Q(18)
Dans le calcul de Q(n)=Q(n-Q(n-1))+Q(n-Q(n-2)), les deux termes Q(n-1) et Q(n-2), donnent deux décalages à partir de n permettant de trouver les indices n-Q(n-1) et n-Q(n-2) des deux termes à ajouter.
Les premiers termes Q(n) sont Q(1)=1, 1, 2, 3, 3, 4, 5, Q(8)=5, Q(9)=6, 6, 6, 8, 8, 8, 10, Q(16)=9, Q(17)=10, Q(18)= ...
Pour calculer Q(18), on observe que les deux éléments précédents sont Q(17)=10 et Q(16)=9.
Au lieu d'ajouter ces deux nombres, comme on l'aurait fait pour une suite de Fibonacci, on se décale de 10 et de 9 crans à partir du rang 18, c.-à-d. en 18-10=8 et en 18-9=9, les deux valeurs à ajouter sont Q(8)=5 et Q(9)=6, d'où Q(18)=5+6=11.
La suite obtenue est bizarre, elle a un comportement modérément erratique, peut-être chaotique, mais ce n'est pas certain, les graphiques laissent penser à une certaine forme de régularité.
Un peu à la manière des suites de Fibonacci et de Lucas, chaque terme est la somme de deux termes précédents, mais pas les deux termes immédiatement précédents :
| Q(1) = Q(2) = 1 et pour n > 2, Q(n) = Q(n-Q(n-1)) + Q(n-Q(n-2)) |
(La définition de la suite de Fibonacci est plus simple : F(n) = F(n-1) + F(n-2)).
| Suite Q de Hofstadter |
|
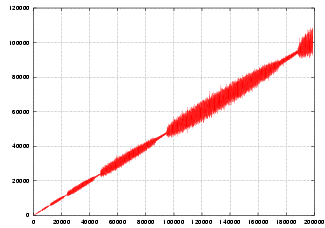
| Termes d'indices 1 à 200 000 (ou 3 500) de la suite Q |
Page avec l'applet java de la suite Q
Exemple : calcul de Q(18)
Dans le calcul de Q(n)=Q(n-Q(n-1))+Q(n-Q(n-2)), les deux termes Q(n-1) et Q(n-2), donnent deux décalages à partir de n permettant de trouver les indices n-Q(n-1) et n-Q(n-2) des deux termes à ajouter.
Les premiers termes Q(n) sont Q(1)=1, 1, 2, 3, 3, 4, 5, Q(8)=5, Q(9)=6, 6, 6, 8, 8, 8, 10, Q(16)=9, Q(17)=10, Q(18)= ...
Pour calculer Q(18), on observe que les deux éléments précédents sont Q(17)=10 et Q(16)=9.
Au lieu d'ajouter ces deux nombres, comme on l'aurait fait pour une suite de Fibonacci, on se décale de 10 et de 9 crans à partir du rang 18, c.-à-d. en 18-10=8 et en 18-9=9, les deux valeurs à ajouter sont Q(8)=5 et Q(9)=6, d'où Q(18)=5+6=11.
La suite obtenue est bizarre, elle a un comportement modérément erratique, peut-être chaotique, mais ce n'est pas certain, les graphiques laissent penser à une certaine forme de régularité.
Une famille de suites du même type
Ces suites peuvent avoir des comportements similaires ou non.
Sélectionnez celle dont vous voulez calculer des termes.
Références, ressources, liens
Hofstadter-type sequences On-Line Encyclopedia of Integer Sequences
Hofstadter's Q-Sequence Eric Weisstein's world of Mathematics
La fonction G de Hofstadter Daniel Krob (Programmes Maple pour illustrer une propriété de G)
Acoustic illusions Endlessly rising melodies: The Shepard effect. It was Douglas Hofstadter's ("Godel, Escher, Bach") idea to apply the shepard effect to Bach's canon.
La suite de Douglas Hofstadter : un paradigme de raisonnement non uniforme. N. Lygeros
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.