Accueil > Mots > Suites > Fibonacci > Fibonacci 3
Suite de Fibonacci
Mise en évidence - Applications
Formules - Propriétés de la suite de Fibonacci
Récurrences linéaires
| Relations | Commentaires |
| F(n)= F(n-1)+F(n-2) | avec F(0)=0, F(1)=1 donne la définition |
| F(n)+F(n+3)=2 F(n+2) | F(n)+F(n+3) = F(n+2)-F(n+1) + F(n+2)+F(n+1) = 2 F(n+2) |
| F(n)+F(n+4)=3F(n+2) | ajouter F(n+4)-F(n+3)=F(n+2) à la précédente |
Générateur de formules
Suivant le principe expliqué ci-dessus, l'application suivante vous fabrique aléatoirement autant de formules que vous le souhaitez entre trois termes
Si le nombre de termes est supérieur à 3, cliquez à nouveau sur [Formule] pour d'autres relations entre les mêmes termes de la suite de Fibonacci.
L'ordre des termes est sans importance mais n'oubliez surtout pas les virgules de séparations.
Une écriture comme 8,4,2,1,-3 convient tout aussi bien que
F(n+ki) au moins où n est une variable et les ki sont connus (par exemple k0 = 8, k0 = 4 ...)
Si le nombre de termes est supérieur à 3, cliquez à nouveau sur [Formule] pour d'autres relations entre les mêmes termes de la suite de Fibonacci.
L'ordre des termes est sans importance mais n'oubliez surtout pas les virgules de séparations.
Une écriture comme 8,4,2,1,-3 convient tout aussi bien que
Fn+8,Fn+4,Fn+2,Fn,Fn-3
Matrices
Propriétés
Démonstrations
Si M est la matrice carrée 2x2 M=[1,1;1,0] (dans la notation ascii utilisée par Pari/gp), alors la matrice M^n est M^n = [F(n+1), F(n) ; F(n), F(n-1)]. (Démonstration simple par récurrence).
Les coefficients de ce tableau forment la suite A094435 de NJAS (réf. dans la marge gauche)
Voir à la page des calculs comment ces matrices ou ces formules sont utilisées pour effectuer des calculs rapides de F(n).
L'application ci-dessous construit les formules de F(2n), F(3n), F(4n), F(5n), F(6n), etc.
Voir à la page des calculs comment ces matrices ou certaines de ces formules sont utilisées pour effectuer des calculs rapides de F(n).
F(n+s) = F(n+1)F(s)+F(n)F(s-1) = F(n)F(s+1) + F(n-1)F(s) F(n+s-1) = F(n)F(s)+F(n-1)F(s-1) et F^(kn) = Sump=0..k C(k,p) F(p) Fp(n)Fk-p(n-1) qui donne en particulier F(n) = F(n) F(2n) = 2 F(n)F(n-1) + F2(n) F(3n) = 3 F(n)F2(n-1) + 3 F2(n)F(n-1) + 2F3(n) F(4n) = 4 F(n)F3(n-1) + 6 F2(n)F2(n-1) + 8 F3(n)F(n-1) + 3 F4(n) ...
Démonstrations
Si M est la matrice carrée 2x2 M=[1,1;1,0] (dans la notation ascii utilisée par Pari/gp), alors la matrice M^n est M^n = [F(n+1), F(n) ; F(n), F(n-1)]. (Démonstration simple par récurrence).
[1 1] [2 1] [3 2] [5 3] [F(n+1) F(n) ]
M = [1 0], M^2 = [1 1] = M+I, M^3 = [2 1] M^4 = [3 2] ... M^n = [F(n) F(n-1)] = F(n)M+F(n-1)I
En effectuant le produit M^n x M^s = M^(n+s) vous obtenez d'une part
[F(n+1) F(n) ] [F(s+1) F(s) ] [F(n+1)F(s+1)+F(n)F(s) F(n+1)F(s)+F(n)F(s-1)]
M^n x M^s = [F(n) F(n-1)] x [F(s) F(s-1)] = [F(n)F(s+1)+F(n-1)F(s) F(n)F(s)+F(n-1)F(s-1)]
ou sans écrire les matrices et en utilisant M^2 = M+I
M^n x M^s = (F(n)M+F(n-1)I)(F(s)M+F(s-1)I) = F(n)F(s)(M+I)+ (F(n)F(s-1)+F(n-1)F(s))M+F(n-1)F(s-1)I
= (F(n)F(s)+F(n)F(s-1)+F(n-1)F(s)) M + (F(n)F(s)+F(n-1)F(s-1))I
= (F(n+1)F(s)+F(n)F(s-1))M + (F(n)F(s)+F(n-1)F(s-1))I
F(n+s) = F(n+1)F(s)+F(n)F(s-1) = F(n)F(s+1) + F(n-1)F(s)
F(n+s-1) = F(n)F(s)+F(n-1)F(s-1)
En particulier on obtient
F(n+s) = F(n+1)F(s) + F(n)F(s-1) = F(n)F(s+1) + F(n-1)F(s)
F(2n+1) = F2(n+1) + F2(n)
F(2n) = F2(n) + 2 F(n)F(n-1) = F(n) (F(n) + 2F(n-1))
En essayant de généraliser et en appliquant la formule du binome (X+Y)^k = sum C(k,p)X^pY^(k-p)
(M^n)^k = (F(n) M+F(n-1)I)^k = Sump=0..k C(k,p) (F(n)M)^p (F(n-1))^(k-p)I
= Sump C(k,p) F^p(n)(F(p)M+F(p-1)I) (F(n-1))^(k-p)I
= Sump C(k,p) F(p)F^p(n)F(n-1)^(k-p) M + (F(p-1)F^p(n)+F(n-1))^(k-p))I
F(kn) = Sump C(k,p) F(p) F^p(n)F^(k-p)(n-1)
par exemple :
F(n) = F(n)
F(2n) = 2 F(n)F(n-1) + F2(n)
F(3n) = 3 F(n)F2(n-1) + 3 F2(n)F(n-1) + 2F3(n)
F(4n) = 4 F(n)F3(n-1) + 6 F2(n)F2(n-1) + 8 F3(n)F(n-1) + 3 F4(n)
On en déduit aussi que F(n) divise F(kn)
F(n) premier entraîne n premier
Les coefficients de ce tableau forment la suite A094435 de NJAS (réf. dans la marge gauche)
Voir à la page des calculs comment ces matrices ou ces formules sont utilisées pour effectuer des calculs rapides de F(n).
L'application ci-dessous construit les formules de F(2n), F(3n), F(4n), F(5n), F(6n), etc.
Voir à la page des calculs comment ces matrices ou certaines de ces formules sont utilisées pour effectuer des calculs rapides de F(n).
Carré d'un nombre de Fibonacci
F(n-1)F(n+1) - F2(n) = (-1)nLa propriété aisément se montre par récurrence.
En premier lieu,
F(0)F(2)-F2(1) = 0-1=-1 = (-1)1montre que la propriété est vérifiée lorsque n=1.
En supposant la propriété vraie jusqu'au rang n, il suffit de transformer l'égalité
F(n-1)F(n+1) - F2(n) = (-1)n
(F(n+1)-F(n))F(n+1) - F2(n) = (-1)n
F2(n+1) - F(n)F(n+1)- F2(n) = (-1)n
F2(n+1) - F(n)(F(n+1)+F(n)) = (-1)n
F2(n+1) - F(n)F(n+2) = (-1)n
F(n)F(n+2) - F2(n+1) = (-1)n+1
Somme des termes successifs de la suite de Fibonacci
Somme (finies) des termes successifs.
Démonstration aisée par récurrence
Somme des termes de rangs pairs. En se ramenant à la forme précédente
Somme des termes de rangs impairs. De même ou en combinant les deux précédentes
Somme entre deux indices
Somme des termes de rangs multiples de 3.
La relation F(5n+10)=11F(5n+5)+F(5n) peut être obtenue plus haut dans la page, on peut aussi trouver une formule générale reliant F(kn+2k), F(kn+k) et F(kn) (l'un des coeffs est un nombre de Lucas L(k) ) pour en déduire la somme S(kn) des F(kj) pour j variant de 0 à n, qui devrait être, sauf erreur,
0+1+1+2+3+5+8+...+F(n-1)+F(n) = F(0)+F(1)+F(2)+...F(n-1)+F(n) = F(n+2) -1
Somme des termes de rangs pairs. En se ramenant à la forme précédente
0+1+3+8+21+...+F(2n) = F(0)+F(2)+F(4)+...F(2n-2)+F(2n)
= F(0)+F(2)+F(4)+F(6)+...+F(2n-2)+F(2n) = F(2n+1) -1
Somme des termes de rangs impairs. De même ou en combinant les deux précédentes
1+2+5+13+...+F(2n)+F(2n+1) = F(1)+F(3)+F(5)+...+F(2n-1)+F(2n+1) = F(2n+3)-F(2n+1) = F(2n+2)Somme alternée.
0-1+1-2+3-5+8+...+F(2n) = F(0)-F(1)+F(2)-F(3)+...-F(2n-1)+F(2n) = F(2n-1) -1
Somme entre deux indices
F(k)+F(k+1)+...+F(r-1) + F(r) = F(r+2)-F(k+1)(Soustraire la somme F(0)+...+F(k-1) de la somme F(0)+...+F(r))
Somme des termes de rangs multiples de 3.
F(0)+F(3)+F(6)+F(9)+...+F(3n-3)+F(3n) = 1/2*F(3n+2)-1/2Somme des termes de rangs multiples de 4.
F(0)+F(4)+F(8)+F(12)+...+F(4n-4)+F(4n) = 1/3*F(4n+5)-1/3On peut chercher simplement les formules
S(kn)=F(0)+F(k)+...+F(kn), ainsi pour
k=5 il suffit d'utiliser F(5n+10)=11F(5n+5)+F(5n) pour trouver la somme
S(5n)=1/11 * (F(5n+5)+F(5n)-5) des termes de rangs multiples de 5.
La relation F(5n+10)=11F(5n+5)+F(5n) peut être obtenue plus haut dans la page, on peut aussi trouver une formule générale reliant F(kn+2k), F(kn+k) et F(kn) (l'un des coeffs est un nombre de Lucas L(k) ) pour en déduire la somme S(kn) des F(kj) pour j variant de 0 à n, qui devrait être, sauf erreur,
Skn = (F(kn+k)-F(kn)-F(k))/L(k) = (F(k)*F(kn+1) + (F(k-1)-1)F(kn)-F(k))/L(k).
Sommes infinies (Séries)
Utilisation de la fonction génératrice pour le calcul de certaines séries, lorsqu'elles convergent.
Sumk>=1 F(k)xk = x/(1-x-x2)Par exemple, pour
x=1/2, on obtient 1/2 F(1)+1/4 F(2)+ 1/8 F(3) +...= 2.
À la rencontre de la suite de Fibonacci
Cubes de Fibonacci
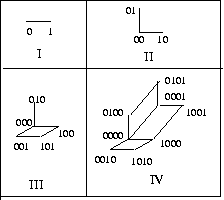
Un cube de Fibonacci est le sous-graphe d'un hypercube dont on n'a gardé que les sommets dont le code binaire n'a jamais deux chiffres 1 consécutifs.
Ces sommets sont donnés par l'application ci-dessous :
On peut aussi construire ces graphes de la manière suivante :
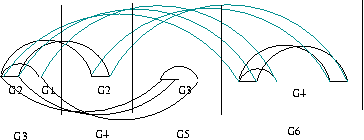
Gn+2 s'obtient à partir de Gn+1 et de Gn en reliant les sommets des deux sous-graphes Gn : le premier qui est dans Gn+1 et le nouveau qui est accolé à Gn+1
Nombre de chemins
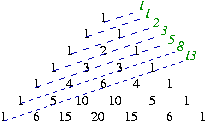
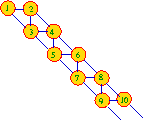 F(n) est le nombre de chemins de la case 1 à la case n si on s'impose
de se limiter aux déplacements vers la droite ou le bas ou les deux
diagonalement : F(n) est le nombre de chemins de la case 1 à la case n si on s'impose
de se limiter aux déplacements vers la droite ou le bas ou les deux
diagonalement :
(1,2,4,5), (1,2,3,4,5), (1,2,3,5), (1,3,4,5), (1,3,5) sont les 5 chemins permettant d'arriver à F(5) donc F(5) = 5. |
Nombre de pavages par des dominos
Un quadrillage nx2 a une longueur de n carreaux et une hauteur de 2 carreaux.
Quel est le nombre K(n) de manières de paver (complètement) ce quadrillage par des dominos (les dominos recouvrent deux cases ayant un côté commun) ?
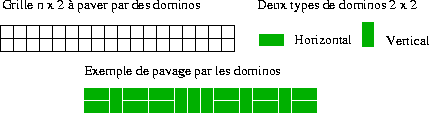
Il est facile de voir que K(1) = 1 (1 domino vertical), K(2) = 1 (2 dominos horizontaux) et K(n+1)=K(n)+K(n-1) et donc que K(n) = F(n).
Pour les nombreux lecteurs qui arrivent ici alors qu'ils recherchent en réalité de 'vrais' dominos à imprimer et à découper, j'ai composé à leur intention une pleine page A4 (PDF) de 28 dominos comme ceux reproduits ci-dessous.

Cliquer
Si vous connaissez une relation, autre que celle donnée plus haut, entre ces 'vrais' dominos et Fibonacci, prévenez-moi.
Quel est le nombre K(n) de manières de paver (complètement) ce quadrillage par des dominos (les dominos recouvrent deux cases ayant un côté commun) ?

Il est facile de voir que K(1) = 1 (1 domino vertical), K(2) = 1 (2 dominos horizontaux) et K(n+1)=K(n)+K(n-1) et donc que K(n) = F(n).
Pour les nombreux lecteurs qui arrivent ici alors qu'ils recherchent en réalité de 'vrais' dominos à imprimer et à découper, j'ai composé à leur intention une pleine page A4 (PDF) de 28 dominos comme ceux reproduits ci-dessous.

Cliquer
Si vous connaissez une relation, autre que celle donnée plus haut, entre ces 'vrais' dominos et Fibonacci, prévenez-moi.
Réflexions d'un rayon lumineux
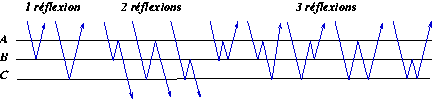
Il revient au même de dénombrer les mots de longueur n écrits à l'aide l'alphabet de trois lettres {A, B, C}. La lettre de rang pair (respectivement impair) est supérieure (respectivement inférieure) à sa suivante.
Le nombre de mots de n lettres est F(n-2).
Somme des carrés
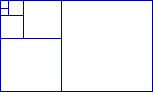
|
La figure ci-contre permet de comprendre l'égalité.
F2(0)+F2(1)+F2(2)+...+F2(n-1)+F2(n)=F(n)×F(n+1)
Démonstration par récurrence.
|
Triangles et Pi
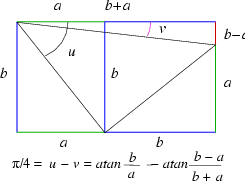
En prenant, c'est possible, pour b-a, a, b, b+a quatre nombres de Fibonacci consécutifs on obtient la relation Pi/4 = atan(Fn+1/Fn) - atan(Fn-1/Fn+2)
En particulier avec 3, 5, 8, 13, on a Pi/4 = atan(8/5) - atan(3/13).
Mais évidemment on pourrait aussi prendre des nombres de Lucas (2,1,3,4,7,11,18,29 ...) ou n'importe quelle suite non nulle vérifiant la même relation de récurrence u(n+1)=u(n)+u(n-1) comme par exemple 1, 7, 8, 15 ... et écrire Pi/4 = atan(8/7) - atan(1/15).
On peut chercher ce que donne la formule lorsque l'on fait tendre n vers l'infini.
Triangle de Pascal
Factorisations des termes de la suite de Fibonacci
Écritures primaires
Les nombres de Fibonacci sont entièrement factorisés jusqu'à l'indice 396 dans un tableau.
On remarquera ceux qui sont premiers : F(3)=2, F(4)=3, F(5)=5, F(7)=13 ...
On remarquera ceux qui sont premiers : F(3)=2, F(4)=3, F(5)=5, F(7)=13 ...
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()